“N号房”折射隐私之殇,看中科院区块链“天眼”如何破局
关于天眼(SkyEye),我们很容易联想到通过监控视频的“天眼”数字监控系统,或者是可查询企业信息的天眼查,抑或是影视作品《终结者》里的天网(Skynet),这些系统有的能够帮助我们查询到有用的信息,有的则会产生非常严重的后果,例如美国版天眼计划棱镜(PRISM)在被斯诺登曝光之后,便引发了全球范围的担忧。
正如现实世界一样,区块链世界也会出现一些违法犯罪的现象,因此对于监管的需求是非常迫切的,但正如棱镜计划一般,赋予监管者过大的权限,可能最终会引发新的灾难。
正是如此,区块链监管必然要进行权衡,既要对潜在的违法行为进行追踪,同时确保监管者不会滥用职权。
这期的学术研究分享,我们会介绍来自中科院学者马天军等人提出的具有监督功能的区块链身份追溯方案BTSOF,该方案是中科院天眼区块链(SkyEye)方案的升级版,在这种架构下,监管机构必须获得委员会的同意,才能对用户数据进行追踪。
而在硬核技术文章精选部分,我们还会看到关于以太坊默克尔树结构切换、密码学原语混淆电路的内容。
另外,在过去的一周当中,比特币闪电网络,以太坊1.X及2.0研发均迎来了一些新的进展。

(图片来自:tuchong.com)
“N号房”引发隐私技术争议,中科院区块链“天眼”如何破局
当前有很多区块链研究专注于隐私保护,然而,对于隐私意识非常淡薄的普通用户而言,强隐私技术的发展,并不一定是件好事。
这是因为,犯罪分子也可利用强大的隐私保护功能来对其犯罪进行掩护,例如最近轰动一时的韩国N号房事件,便是这样的例子,其主犯赵主彬主要利用隐私币门罗及Telegram来隐藏其交易痕迹,在这起事件当中,庆幸的是犯罪分子使用了加密货币交易所,因此暴露了他们的身份,若假设他们并未使用这些第三方工具,则会给破案带来巨大的阻力。
也因此,关于区块链身份可追溯机制的研究,似乎在当前的背景下,要显得更为重要一些。
1、1 关于区块链身份可追溯机制的研究
针对保护隐私的区块链项目,一些研究者提出了自己的身份追溯机制,比如:
Ateniese和Faonio 提出了一种针对比特币的身份追溯方案,在他们的方案中,如果用户从可信证书颁发机构获得经认证的比特币地址,则该用户就是经认证的。然后,监管机构就可通过证书颁发机构,来确认比特币交易用户的身份,这种方案与交易所的KYC方案有一些类似。
Garman,Green和Miers则基于Zerocash构建了一个去中心化匿名支付系统,他们的方案通过添加隐私保护策略执行机制来实现追踪。
Narula,Vasquez和Virza则设计了一个称为zkLedger的分布式账本,其可以提供强大的隐私保护、公共可验证性及可审核性,他们的方案主要用于审核某些银行的数字资产交易。据悉,账本在zkLedger中是以表格的形式存在,每个用户的身份对应于表中的每一列,因此,监管者可据此来确定每个用户的身份。
而来自中科院的Tianjun Ma等人则提出了SkyEye(天眼),这是一种可追溯用户身份的区块链方案,其允许监管机构追踪区块链用户的身份,而没有任何限制,因此存在监管滥用的可能。
而在最新的研究中,信息安全国家重点实验室的研究者Tianjun Ma、Haixia Xu以及Peili Li基于SkyEye提出了一种具有监督措施的区块链身份追踪方案,简单来说,监管机构必须要在获得委员会同意的情况下,才能对用户数据进行跟踪。
论文链接:https://eprint.iacr.org/2020/311.pdf
此外,研究者构造了一个非交互式可验证的多秘密共享方案(VMSS方案),并利用VMSS方案为Cramer-Shoup公钥加密方案设计了一个分布式多密钥生成(DMKG)协议,这也是BTSOF所采用的一个协议。
1、2 关于区块链天眼(SkyEye)
在中科院的天眼(SkyEye)区块链方案设计中,使用了一些密码学原语(例如chameleon哈希函数方案),SkyEye由多项式时间算法(Setup,Geninfo,Verinfo,Genproof,Verproof以及T race)组成,其中Setup为系统生成公共参数pp,Geninfo和Verinfo分别创建和验证用户注册信息,Genproof和Verproof分别生成和验证用户的身份证明,而T race算法则在区块链数据中跟踪用户的真实身份。

reginfo后,这个reginfo信息就会发送给监管机构。如果reginfo的信息验证成功,则监管者可以从reginfo中提取一些信息recordu =(PKcu,IDu,CHidu),并将其存储到数据库(Database)中,同时把PKcu和CHidu信息添加到Merkle树(MT),并广播这些信息,如果用户u的(PKcu ||CHidu ) 出现在Merkle树(MT)中,则表明其注册成功,然后,用户u可以生成区块链数据datau,这些数据发送到节点网络(由普通节点和验证节点组成),与区块链中的传统验证过程不同,这里的验证过程验证的是:
- 数据内容;
- 数据中的身份证明;
监管者从区块链获取datau数据,并通过使用私钥skreg解密datau中的chameleon哈希公钥的每个密文,以获得chameleon哈希公钥集PKc,最后,监管者可以根据PKc搜索数据库,从而在datau中获取用户的真实身份集ID。
而这样一个系统,就用到了这些密码学原语:Cramer-Shoup加密方案 、非交互式零知识 、数字签名方案 以及多秘密共享方案(关于这些密码学组件的具体描述,可以看原论文);
对于SkyEye方案,监管者进行追踪的前提条件,是使用可追溯的私钥skreg对区块链数据datau中的所有chameleon哈希公钥密文进行解密,以获得chameleon哈希公钥集PKc。
然而在SkyEye方案中,监管机构的权力过大成为了一个主要问题,其可以任意跟踪区块链用户的身份,而不受任何限制和监督,从而引发了一些担忧。
1、3 具有监督功能的区块链可追溯方案(BTSOF)
为了监督监管机构,研究者提出了新方案BTSOF,其主要设计思想如下图所示:

datau和相应的证据witu发送给委员会。如果委员会同意追踪,则它将把追踪信息发送给监管机构,最后,监管机构可以根据委员会发送的信息追踪数据datau。
上面提到,SkyEye方案中使用了Cramer-Shoup加密方案,而在新方案中,则是让委员会定期生成Cramer-Shoup加密方案的可追溯公私钥对,换句话说,监管机构必须获得委员会的同意才能进行追踪,这相当于起到了一个监督的作用。
而在这个过程中的关键,是一种称为DMKG的加密协议,其是研究者基于分布式密钥生成协议DKG,为Cramer-Shoup加密方案而设计的,其负责生成的是委员会的可追溯公私钥对。
1、4 BTSOF的威胁模型,目标及构造
在BTSOF方案中,我们要考虑的一个威胁模型,就是委员会非诚实成员的比例,如果对手控制了超过1/3的委员会成员,则可能对最终结果构成威胁。
而BTSOF的目标,是确保监管机构必须获得委员会的同意才能进行跟踪,并且只能跟踪发送给委员会的数据集,那这又是如何实现的呢?
它的关键思想描述如下:
监管机构向委员会广播一条消息,指出其要跟踪的数据集,而消息有两种类型:
-
消息
mrtc = (R, dw) = (R,(datal, witl)l∈{1,...,len})表示监管机构希望使用len元素跟踪数据集,其中R表示监管机构的标识符,以及(datal,witl)表示第l个数据,和l∈{1,...,len}的相应证据。 -
消息
mrtc =(R,dw)=(R,(T,witT))表示监管机构想要追踪T周期的所有数据,其中R表示监管机构的标识符,而witT表示相应的证据。
Pi收到上述消息mrtc后,对于每个i∈Qfinal,Pi都会验证mrtc中相应证据的正确性。如果验证成功,Pi在消息mrtc中对dw签名,然后将签名发送给监管机构。每次收到委员会成员的签名时,监管机构都会对签名进行验证,如果验证成功,则将其保存在集sigall当中。
最后,如果sigall的大小大于或等于t,则监管者将消息mrtc =(R,dw,sigall)广播给委员会。
在收到上述消息mrtc =(R,dw,sigall)之后,Qfinal中的每个委员会成员首先验证集sigall中的每个签名,并计算有效签名的数量。 如果该数字大于或等于t,则Qfinal中的委员会成员会执行一些操作。
监管者在接收到诚实成员Pi为i∈Qfinal发送的消息mi后,选择这些消息中占多数的值,并根据该值进行追踪。
洒脱喜简评:区块链隐私保护与监管看似相互矛盾,实际是可以做到两者兼得。天眼升级版协议BTSOF在确保普通用户的隐私前提下可打击犯罪行为,同时确保不会造成监管权力过大的问题,而实现这个目标,就依托于各种密码学工具的组合,而类似这样的方案,会更容易被大众和监管机构所接受。
二、硬核技术文章一周精选
2、1 以太坊 2020:路线图与展望
以太坊在 2020 会带来什么惊喜?
你可能错过了一条消息,Vitalik Buterin 在推特上发了一个《个人心目中的以太坊路线图》。那么你是否也好奇他发表的图片是什么意思,今年的以太坊有哪些看点?
我使用超链接为他发表的图片添加了超链接,仅此我们也可预览以太坊 2020 年可能出现的亮点。
双剑合璧:用权益证明和分片扩展以太坊的吞吐量
这里是一份用超链接标注后的 Vitalik 个人以太坊路线图。链接的选择,当然由我自己承担,图解则仍归功于 Vitalik。
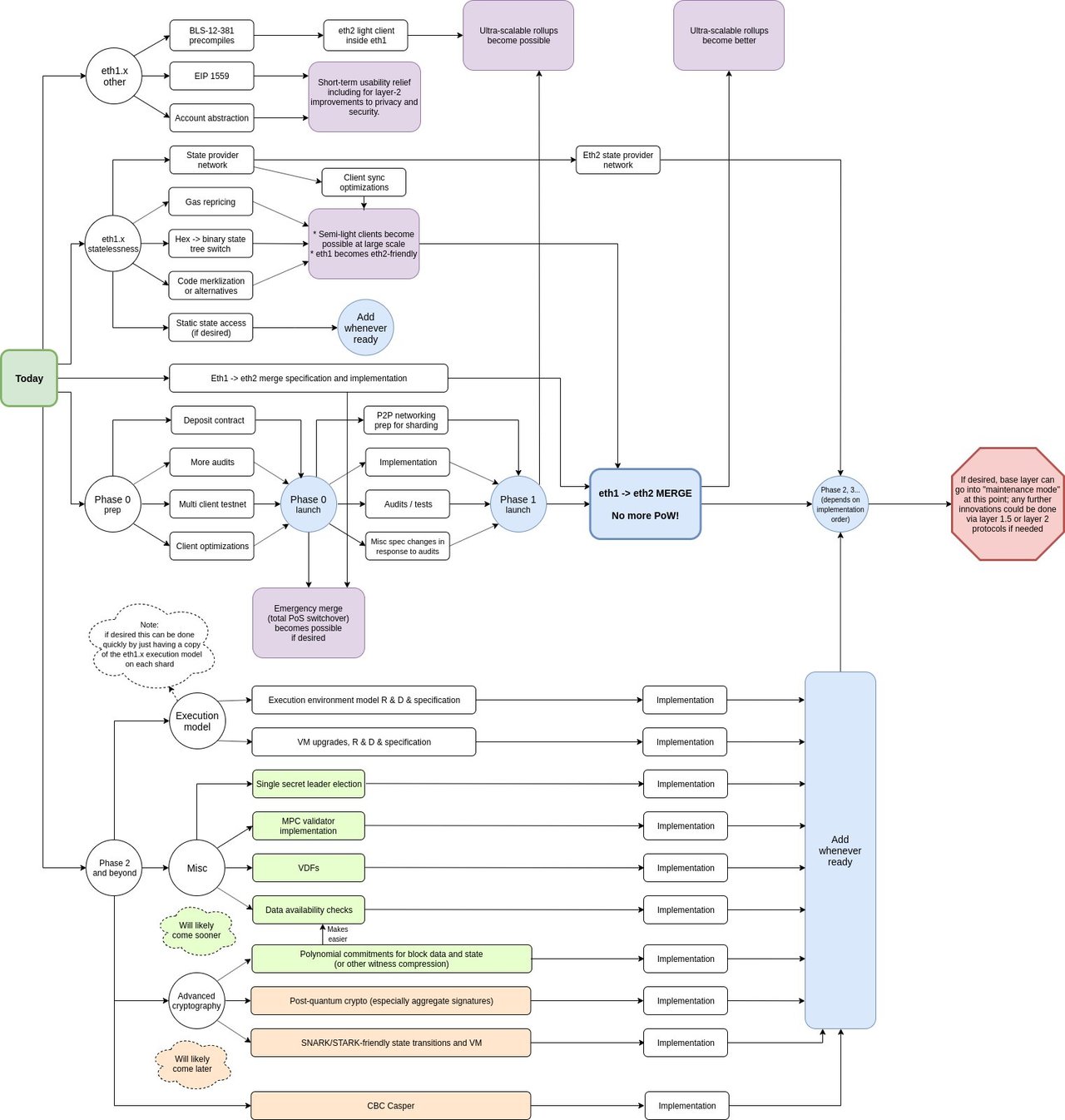
- 译者注:此处的图片不能展现出作者加上的超链接,仍是 Vitalik 发表的原图。欲了解作者加入的超链接,请阅读原文 -
这幅图里面有四大块,从上到下分别是:
- “以太坊 1.x 杂项”
- “以太坊 1.x 无状态性”
- 一个从 Eth2 Phase 0 到 eth1->2 合并、围绕着移除工作量证明(PoW)的 “核心”
- eth2 Phase 2 及以后
- Eth2 Phase 1 启动
- eth1 -> eth2 合并的技术设想和实现
- Eth 1.x 无状态性
大合并是以太坊可扩展性的巨大飞跃,需要庞大的工程工作来支撑其可能性、使其能安全、稳妥地运行。上述前提即点出了工作上的分类。
关于大合并及其它问题,还有很多可讨论的。蛋在这里我们只讨论核心进展及 “以太坊 1.x 杂项”,因为它们与以太坊的 2020 关联较大。我们就从以太坊 2.0 Phase 0 开始。
Ethereum 2.0 Phase 0
极有可能在 2020 年上线的部分是信标链。
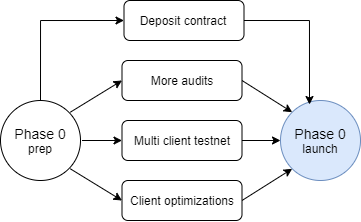
信标链启动的主要前提是:
- 在 Eth1 主链上部署 Eth2 保证金合约;
- 至少 2 个,理想情况下应该有 3 个 Eth2 客户端团队,推出了可用于生产环境的软件版本
- 保证金合约发布之后,至少有 16,384 名验证者存入保证金(其中的金额累计至少有 524,288 ETH)
Danny Ryan、Diederik Loerakker,还有四个团队,都一直在构建能用于生产的 Eth2 客户端。(按字母顺序排列)正在构建的客户端有:Lighthouse、Nimbus、Prysm、Teku、Trinity。
以太坊基金会,以及其他团队(比如 Artemis、Harmony、Lodestar、Nethermind 还有 Parity),还有那些开发质押服务的供应商,乃至初来乍到的新人,对此也都有不同程度的贡献。还有一些审计工作正在进行。
在 2020 年发布信标链的使命是清晰的,精力也是集中的。大部分工作都已经用分布式的方式完成了。
从经济角度来看,用(超过 20% 的 年化收益率(APR)来吸引 16,384 名验证者(524,288 ETH),不论用什么办法,都是很有吸引力的(同时,年化收益率会随着验证者数量的增加而下降)。
- 来源:上面超链接所包含的验证者收益率计算器 -
如何为信标链的 2020 作贡献?
信标链客户端的生产版本预计会在多重审计切多客户端测试网能稳定运行一段时间后发布;多个单客户端测试网已经稳定运行了一段时间,虽然仍需要做高负载下的优化及调试工作。
以太坊永远欢迎更多贡献者。需要贡献的领域包括:客户端的点对点网络组建、客户端互操作性、常用的测试工具、客户端及网络的安全性、性能和稳定性。
黑客、安全性、EVM 和智能合约领域的专家们,审计保证金合约并评估运行时验证(Runtime Verification)的工作永远需要你们的帮助,虽然保证金合约的字节码还未部署到主链上,你可以先行一步,因为预计保证金合约不会有什么变化了。
以太坊 1.x 需要帮助
这份图解最顶端的一部分 “以太坊 1.x 杂项”,是跟当前的以太坊主网相关的部分。
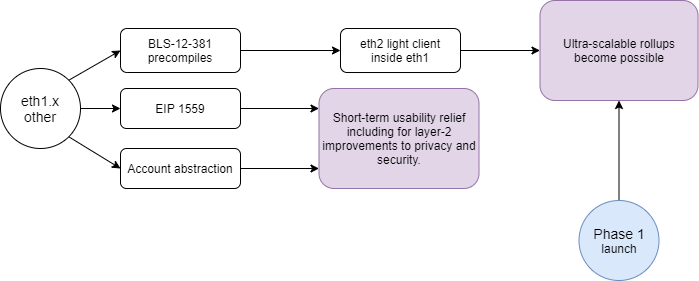
这部分可分为三个项目,粗略来说就是三个 EIP,需要有执着的贡献者,才有可能在 2020 年部署到主网上。
BLS12-381 的预编译已经由 Matter Labs 的 Alex Vlasov 提了好几个月,EIP2537 也正在撰写中。EIP 2537 添加了对 Eth2 所用的 BLS12-381 曲线的支持,使得智能合约可以成为 Eth2 的轻客户端。有了对 BLS12-381 曲线的预编译之后,新的智能合约就能验证来自 Eth2 分片的数据。Eth2 Phase 1 启动时会引入分片,可以提高 Eth1 上的 Rollup 方案的数据可用性。Rpllup 方案其实就是一种智能合约,其 大部分计算和存储都是放在链下 的,但一些数据会发到链上,以备不时之需。如果数据可用性没有平均,Rollup 的吞吐量就能变得更大。有 Alex Vlasov 的工作,BLS12-381 的预编译很有可能在 2020 年引入(甚至可能比信标链更早推出)。
EIP-1559 可能会给用户带来一些好处,因为用户将可在发交易时 忽略 Gas 费的设置,勇士又能保证 不会支付过高手续费,不会等待超乎常理的延迟。该 EIP 写道:“预计大部分用户将不再需要手动设置 Gas 费,哪怕网络中的交易活动很频繁。”此外,该 EIP 还包括了燃烧手续费的设置,这就有利于对冲 ETH 的通缩,但又无需大幅削减矿工的收益。自该 EIP 在一年前提出以来,已经有人为此做了一些工作,不过,现在没有人挺身主导这个工作。
账户抽象化则是让用户能创建出具备任意授权逻辑的帐户(译者注:使账户的创建能脱离以太坊协议本身的束缚)。其中附加的灵活性可能影响深远,我们这里举个例子:一个多签名智能合约钱包可以用自有资金来支付它的交易的 Gas 费。只要有了一个钱包、里面有资金,就不再需要另一个持有 ETH 的账户来跟这个钱包交互并支付 Gas。账户抽象化的提法可以追溯到 2015 年,但一个月前的一份提案使得在 2020 年有可能实现账户抽象化。
如果你想了解更多或作出贡献,请参与 https://gitter.im/ethereum/AllCoreDevs(这是核心开发者之间的一个聊天室)。
“以太坊 1.x 无状态性” 也需要支持,但这是一个很大的话题,你可以看看这份为 “无状态以太坊” 提议的路线图,还有以太坊基金会博客的 “1.x Files” 系列。
向 Geth 团队致敬
上周,Geth 团队在 Github 上放出了第 164 个版本。我们不应忘记,Geth 团队一直在给以太坊 Geth 客户端增加功能、作出改进和优化。人们很容易把他们的工作当成理所当然的,而忘了他们付出的努力。让我们一起致敬(排名仅按字母,不分先后)Guillaume Ballet、Zsolt Felföldi、Felix Lange、Gary Rong、Adam Schmideg、Martin Holst Swende 还有 Péter Szilágyi!
Felix、Martin 和 Péter 已经做了很多年的 Geth 优化及升级工作,最早可追溯到 “上海攻击” 时期(那时的队友包括 Nick Johnson 和 Jeffrey Wilcke)(译者注:“上海攻击” 是指 2016 年 Devcon2 在上海举办期间在以太坊网络上爆发的 DoS 攻击)。
几个月以前,Péter 作为嘉宾参加了 ConsenSys 举办的一个开发者圆桌。他分享了一些对 Eth2、无状态性、贡献者激励措施的看法,也谈到了他所赞赏的人(在超链接所附视频的第 49 分钟)。谢谢你的提醒,Péter,也谢谢你和你的团队所做的重要工作。
想感谢他们、学习他们或者为 Geth 贡献的话,请加入 Go Ethereum 的 Discord 频道。
以太坊 2020 及其他
从当前来看,以太坊上可能发生的进展的粗略顺序如下:
- 信标链(Eth2 Phase 0)在 2020 年推出
- LS12-381 曲线预编译在 2020 年推出(也许这个才是最早推出的)
- 如果有人来推动账户抽象化和 EIP 1559,他们有可能会在 2020 年推出
- Eth2 Phase 1
- Eth 1.x 无状态性
- eth1 -> eth2 大合并
- (后续)执行模式、隐私和安全性提升、高级密码学元件
我觉得在后面的文章中我也会加入致谢部分。那么我下一个要感谢的是 Solidity 团队。他们会在 2020 Solidity 峰会上致开幕辞。
(完)
原文链接: https://ethos.dev/ethereum-2020-roadmap/ 作者: ethos.dev 翻译: 阿剑
来源链接:https://www.8btc.com/article/576260
2、2 以太坊核心开发者:MPT十六叉树将被替换
想象一下,你正在翻译一本5000页的书籍,作者一直打电话告诉你他对故事做了调整,这会影响到你已经翻译过的页面……而这可能会一直持续下去,这就是以太坊从当前使用的MPT十六叉树转变为二叉树结构中遇到的一个类似困境。对此,以太坊核心开发者Guillaume Ballet提出了一种方案,可以在大约几天的时间内,通过3个步骤完成这一转换手术。

(图片来自:tuchong.com)
对于该提案,以太坊联合创始人vitalik评论称:“来自Ballet的重要研究基础,它会使以太坊无状态变得友好,同时创造了一个机会,以大大简化该协议。期待在未来的几个月中,来自以太坊1.x开发人员更加出色的工作及成果。”

以下是译文:
影响以太坊的众多问题之一是账户和合约数据的存储方式,以太坊目前选择的结构称为默克尔帕特里夏树(Merkle Patricia Tree,或简称MPT)。尽管从理论上讲,它是很有意义的,但在实践中,它带来的问题要比其解决的问题要更多。多年来,核心开发人员一直在讨论向二叉树(binary tree)的转换,在本文中,我将阐明我对这一问题的看法,然后给出一个解决它的方法。
提议的过程引入了一个过渡期,在此期间,两种树结构都会存在。这样做的好处是,在转换树结构时,主链可以保持运行,并且还可以确保将所有帐户转换为二叉树格式。
背景
目前,以太坊的账户是被存储到一棵十六叉树当中的。所谓十六叉,就表示一个节点有16个子节点,理论上这是很好的,因为这意味着你需要更少的"阶段"来存储你所有的数据。
例如,这就是以十六叉树的形式表示键与值对(170,v)的过程。在十六进制中,170表示为0xaa,因此你只需要两层:其中之一用于第一个a,另一层则用于第二个a。

图1: 这是一棵十六叉trie树示例,显示了值“v”如何存储在键0xaa处。此树只有2字节长的键,并且只沿0xaa键的子树被展开。为了简洁起见,不相关的子树被替换为“…”。
170表示为10101010。

图2: 和图1中相同的键值对,以二叉树形式进行存储。为了简洁起见,不相关的子树被表示为“…”。
你可以看到,这棵树要深得多,也窄得多。
在以太坊中,每个区块都包含一个stateRoot字段,它是MPT根的哈希值。总而言之,这个哈希,是通过对根的16个子项的哈希列表进行哈希运算而获得的。这些子哈希列中的每一个,又依次是其子哈希列表的哈希,依此类推。
每次生成一个新区块时,矿工都会更新帐户树并重新计算其根哈希值。哈希存储在新区块的stateRoot字段中,然后新区块被密封。
 图3 区块头的state root字段指向十六叉树的根。
图3 区块头的state root字段指向十六叉树的根。
在十六叉树中,通常每个阶段要获取15个同级哈希。在上面的示例中,这就是30个哈希。
即使更深入,二叉树每个阶段也只需要一个同级哈希。在上面的示例中,就只有8个哈希!这就是为什么在实践当中,二叉树实际上要更好的原因。
覆盖转化法
不幸的是,要将以太坊从十六叉树切换到二叉树,并不是一件容易的事。有很多数据需要转换,并且执行更改需要花费超过15秒的区块时间。
除此之外,想象一下,你正在翻译一本5000页的书籍,作者一直打电话告诉你他对故事做了调整,这会影响到你已经翻译过的页面……而这可能会一直持续下去。
这就是目前以太坊遇到的问题,因为用户可以更新已转换的地址,这意味着你必须重新开始转换过程。
解决此问题的建议是设一个过渡期,在此期间,在十六叉树的顶部放置一棵覆盖二叉树,它的作用是保存状态发生的所有更改,直到基树转换为二叉树。
这种过渡会分成三步进行:
第1步-转换
在这种方法中,确定在区块高度H1处,区块具有两个stateRoots:一个用于“基础”十六叉树,一个用于“覆盖”二叉树。

图4: 在转换过程中,区块具有2个状态根(state Root):一个是传统十六叉树的只读根,第二个是“覆盖”二叉树的根。
十六叉树被认为是只读的,因此对状态的任何更新都将是对覆盖树的更新。
当一笔交易读取或更新一个帐户时,系统首先搜索覆盖树。如果在那里找不到帐户,系统将在旧的十六叉树中搜索该值。
而在同时,十六叉树正在后台转换。现在可以不用担心插入,因为所有更改都存储在顶部树中。
第2步-基转换
后台转换过程完成后,矿工将通过转换结果替换只读的十六叉树基础根来宣布他们已准备好进行切换。对状态的读写操作与步骤1相同。

图5:转换的第二个阶段,区块头将十六叉树基础根替换为其二叉树转换基础根,以向网络发送信号,告知它们已准备就绪。
当一个足够大的序列区块对转换后的基础根具有相同的值时,这意味着大多数矿工都完成了转换,并对转换后的树的外观达成了共识。接下开,就进入到合并过程。第3步-合并两颗树
合并过程会逐渐进行:每次生成新区块时,都会从叠加层中删除n个键,然后将其重新插入到基础树中。该过程将持续进行,直到从叠加层中删除所有键为止。在此阶段,覆盖状态根将从区块头中删除。除此之外,如果交易执行写入覆盖树中找到的键,则该键将从覆盖树中删除,并直接写入到基础树。
下一步
我们已经创建了一个初步的原型,以便估计完成转换所需的时间。我们相信,整个过程可以在合理的时间内(大约几天)完成。随着算法的改进,我将发布更多的细节。
致谢
这项提议得益于Alexey Akhunov,Vitalik Buterin,Anna George,Sina Mahmoodi,Tomasz Stanczak以及Martin H. Swende提供的宝贵意见。
相关讨论:https://ethresear.ch/t/overlay-method-for-hex-bin-tree-conversion/7104
来源链接:https://www.8btc.com/article/575138
2、3 Vitalik:混淆电路(Garbled circuits)快速入门
注:原文作者是以太坊联合创始人Vitalik Buterin。
特别感谢Dankrad Feist对本文进行的审阅工作。
混淆电路(Garbled circuits)是一种非常古老,且非常简单的密码学原语。它们很可能是通用“多方计算”(MPC)的最简单形式。
以下是该方案的常规设置:
-
假设存在两方,爱丽丝(Alice )和鲍勃(Bob),他们想要计算一些函数
f(alice_inputs, bob_inputs),这需要从双方那获取输入。爱丽丝(Alice)和鲍勃(Bob)都想知道计算函数f的结果,但是爱丽丝(Alice)不想鲍勃(Bob)知道她的输入,而鲍勃(Bob)则不想爱丽丝(Alice)知道他的输入。理想情况下,除了f的输出外,他们都不会得知任何其它东西。 - 爱丽丝(Alice )执行特殊的过程(“混淆”-garbling)来加密评估函数f的电路(意味着一组“与”、“或”门)。她将输入(也以与加密电路兼容的方式进行加密)传递给鲍勃(Bob)。
- 鲍勃(Bob)使用一种称为“1-of-2茫然传输(Oblivious Transfer)”的技术来学习自己输入的加密形式,而不让爱丽丝(Alice )知道他获得了哪些输入。
- 鲍勃(Bob)在加密数据上运行加密电路,得到答案,并将其传递给爱丽丝(Alice )。
那基本方案如何运作呢? 让我们从电路开始:

现在,让我们对电路进行加密。首先,对于每个输入,我们随机生成两个“标签”(256位数字):一个表示输入为0,另一个表示输入为1。然后我们也对每个中间线做同样的操作,不包括输出线。注意,这些数据不是爱丽丝(Alice )发送给鲍勃(Bob)的“混淆”的一部分;到目前为止,这只是设置。

enc(out, in1, in2) = out + hash(k, in1, in2),其中k是门的索引(它是电路中的第一个门,第二个,第三个?)。如果你知道这两个输入的标签,并且你有混淆(garbling),那么你可以学习相应输出的标签,因为你只需计算相应的哈希,并将其减去即可。
这是第一个异或门(XOR gate)的混淆(garbling):


爱丽丝(Alice )将提供给鲍勃(Bob)的混淆(garbling)只是每个门第三列中的所有内容,每个门的行被重新排序(以避免显示给定的行是否对应于任何一行中的0或1)。为了帮助鲍勃(Bob)了解为每个门解密哪个值,我们将使用一个特定的顺序:对于每个门,第一行变为两个输入标签均为偶数的行,第二行第二个标签为奇数,第三行第一个标签为奇数,第四行两个标签均为奇数(我们故意选择较早的标签,以便每个门在一个输出上都具有偶数标签,而在另一个输出上具有奇数标签)。我们以相同的方式混淆电路中的每个其他门。
总之,爱丽丝(Alice )为电路中的每个门向鲍勃(Bob)发送了四个 约256位的数字。事实证明,4远非最佳值;有关如何将与门(AND gate)的数量减少为3甚至是2,以及将异或门( XOR gate)数量减少为零,请参见此处的一些优化。请注意,这些优化确实依赖于某些更改,使用XOR代替加法和减法,尽管为了安全起见还是应该这样做。
当鲍勃(Bob)收到电路时,他向爱丽丝(Alice )索要与她的输入相对应的标签,并且他使用称为“1-of-2茫然传输”的协议来向爱丽丝(Alice )索要与自己的输入相对应的标签,而没有向爱丽丝(Alice )透露他的输入是什么。然后他一个接一个地通过电路中的各个门,揭露每个中间门的输出线。
假设爱丽丝(Alice )的输入是两条左线,她给出(0,1),而鲍勃(Bob)的输入是两条右线,他给出(1,1)。这又是带有标签的电路:

- 在一开始,鲍勃(Bob)知道标签6816, 3621, 4872, 5851;
- 鲍勃(Bob)评估第一个门,他知道6816和4872,因此他可以提取与(1,6816,4872)对应的输出值(请参见上表)并提取第一个输出位1;
- 鲍勃(Bob)评估第二个门,他知道6816和4872,因此他可以提取与(2,6816,4872)对应的输出值(请参见上表)并提取标签5990;
- 鲍勃(Bob)评估第三个门(异或门),他知道他知道3621和5851,并学习7504;
- 鲍勃(Bob)评估第四个门(或门),他知道3621和5851,并学习6638;
- 鲍勃(Bob)评估第五个门(与门),他知道3621和5851,并学习7684;
- 鲍勃(Bob)评估第六个门(异或门),他知道5990和7504,并学习第二个输出位0;
- 鲍勃(Bob)评估第七个门(与门),他知道5990和6638,并且学习了8674;
- 鲍勃(Bob)评估第八个门(或门),他知道8674和7684,并学习了第三个输出位1;
请注意,加法的使用在混淆电路中是毫无意义的,因为知道101的鲍勃(Bob)可以减去他自己的输入并得到101 - 11 = 10 (爱丽丝的输入),从而破坏了隐私。 但是,一般情况下,混淆电路可用于不可逆的计算,因此请勿以此方式破坏隐私(例如,人们可能会想到一种计算,其中爱丽丝的输入和鲍勃的输入,是他们对个性测验的答案,而输出是一个位,决定算法是否认为它们是兼容的;而这一位的信息不会让爱丽丝和鲍勃知道彼此的个人测验答案。
1-of-2茫然传输(oblivious transfer)
现在让我们更多地讨论1-of-2茫然传输(oblivious transfer),这是鲍勃(Bob)用来从爱丽丝(Alice )那获取与他自己输入对应标签的技术。问题是这样的:聚焦于鲍勃(Bob)的第一个输入位(第二个输入位的算法相同),爱丽丝(Alice )有一个对应于0(6529)的标签,和一个对应于1(4872)的标签。鲍勃(Bob)有他想要的输入位:1。鲍勃(Bob)想学习正确的标签(4872),而又不让爱丽丝(Alice )知道他的输入位是1。平凡的解决方案(爱丽丝只向鲍勃发送6529和4872)不起作用,因为爱丽丝(Alice )只想放弃两个输入标签中的一个,如果鲍勃(Bob)同时接收两个输入标签,则可能泄漏爱丽丝(Alice)不想放弃的数据。
下面是一个使用椭圆曲线的简单协议:
-
爱丽丝(Alice )生成一个随机椭圆曲线点
H; -
鲍勃(Bob)生成两个点
P1和P2,要求P1 + P2等于H。鲍勃(Bob)选择P1或P2为G * k(即他知道对应私钥的点)。请注意,P1 + P2 = H的要求可确保鲍勃(Bob)不能生成P1和P2。这是因为如果在鲍勃(Bob)知道k1和k2的情况下,如果P1 = G * k1和P2 = G * k2,则H = G *(k1 + k2),因此这意味着鲍勃(Bob)可提取H的离散对数(或“对应的私钥” ”),这意味着椭圆曲线密码系统的所有部分都被破坏了; -
爱丽丝(Alice )确认
P1+P2=H,并使用一些标准公钥加密方案(例如El-Gamal)加密P1下的v1和P2下的v2。鲍勃(Bob)只能解密这两个值中的一个,因为他知道最多对应一个值(P1,P2)的私钥,而爱丽丝(Alice )又不知道是哪一个。
应用领域
混淆电路(Garbled circuits)对于很多应用都有潜在的用途,而不仅仅是2-of-2的计算。例如,你可以使用它们进行任意复杂度的多方计算,其中任意数量的参与者提供输入,这些输入可以在恒定数量的交互中运行。产生一个混淆电路是完全并行的,你可以同时进行多个混淆门。
因此,你可以简单地进行大规模多方计算,其中许多参与者计算电路中所有门的混淆(garbling),并发布与其输入对应的标签。标签本身是随机的,因此不会透露任何关于输入的信息,但是任何人都可以执行公布的混淆电路,并在“清除”中学习输出。有关使用混淆(garbling)作为成分的MPC协议的最新示例,请参见此处。
多方计算不是唯一的应用环境,在这种情况下,这种将计算拆分为可并行处理部分的技术可对秘密数据进行操作,然后再进行可明确运行的顺序部分,这是有用的,而混淆电路并不是实现这一点的唯一技术。一般来说,关于随机编码的文献,包括很多更复杂的技术,这一数学分支在函数加密和模糊处理等技术中也是很有用的。
原文:https://vitalik.ca/general/2020/03/21/garbled.html
作者:Vitalik Buterin
翻译:洒脱喜
稿源(译):巴比特资讯(http://www.8btc.com/article_572746)
- 免责声明
- 世链财经作为开放的信息发布平台,所有资讯仅代表作者个人观点,与世链财经无关。如文章、图片、音频或视频出现侵权、违规及其他不当言论,请提供相关材料,发送到:2785592653@qq.com。
- 风险提示:本站所提供的资讯不代表任何投资暗示。投资有风险,入市须谨慎。
- 世链粉丝群:提供最新热点新闻,空投糖果、红包等福利,微信:juu3644。





 初代韭菜
初代韭菜






